Quand on mesure un objet, il n'y a pas à tortiller : un centimètre est un centimètre ! Pour le dessiner ensuite, on divise chaque centimètre par 10 par exemple pour qu'il "tienne" sur une feuille.

Et pour représenter des choses énormes sans perdre trop de détails ? On appelle l'échelle logarithmique à la rescousse !
(... en se méfiant - quelle que soit l'échelle - de ce que l'on "croit voir" sur un graphique)

 
Échelle linéaire

En fait, l'échelle linéaire, vous connaissez : c'est celle qui se trouve sur vos règles d'écolier, les mètres-ruban de couturière, les mètres-enrouleur de bricolage, bref, à peu près partout...

Le principe est simple : on copie à l'identique un centimètre... puis on double la distance pour arriver à 2, on la triple pour arriver à 3, etc...
La mesure maximale à laquelle on arrive dépend de la taille de l'instrument.

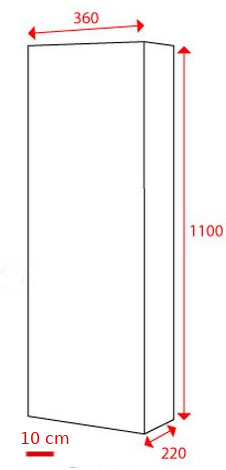Dessiner un objet sur une feuille : changer d'échelle

Une fois qu'on a mesuré les dimensions d'un meuble par exemple, on peut ensuite le dessiner sur une feuille, avec une petite astuce : là où on a mesuré 5 cm, on dessinera une longueur de 1 cm ou 0,5 cm,... histoire que le meuble "rentre" sur la feuille.

Cette opération - qui s'appelle un changement d'échelle - se fait en divisant simplement chaque mesure par 5, ou 10,...

Pour faire le plan d'un pays ou d'une ville, c'est le même principe.
On décide que 10 mètres seront par exemple dessinés sur 1 cm : on divise tout par 1 000 dans ce cas et on appelle cela une carte au millième (1/1000^e).

Cela peut servir aussi pour des objets, comme les circuits de trains réalistes : on réduit chaque objet en respectant les proportions.
Le modélisme utilise beaucoup des formats au 1/87^e : chaque centimètre de maquette reproduit ce qu'il y a sur 87 cm de la vraie locomotive...

 
Échelle logarithmique

Mais pour représenter des choses qui font intervenir des tailles très très différentes, l'échelle linéaire n'est pas une bonne option !

Cela peut être le cas si on veut représenter des situations où il y a une taille donnée mais aussi des choses énormes ou au contraire minuscules, que l'on voudrait mettre sur la même image .

On utilise alors une autre échelle, qui est multipliée par 10 à chaque fois que l'on avance d'une unité : l'échelle logarithmique.

(en cliquant sur l'image, elle s'ouvrira en grand dans un nouvel onglet)

On a ainsi pu représenter l'Univers - oui, tout l'Univers ! - sans que la Terre ne soit un point micro-microscopique !
Une image de l'Univers

Représenter sur un graphique des choses qui évoluent beaucoup

L'échelle logarithmique sert en fait surtout beaucoup pour représenter des choses qui changent énormément avec le temps : si vous voulez mettre dans un graphique une population de lapins qui se multiplie par 20 chaque année par exemple !

Pour représenter cela sur un graphique, on va placer le numéro de l'année sur l'axe des "x" , de 1 à 10.
Mais pour l'axe des "y" ?
Si on choisit une échelle linéaire qui va jusquà jusqu'à 1 024 000 000 000, on perd totalement de vue le nombre de lapins jusqu'à la neuvième année !
Par contre, avec une échelle logarithimique, on voit le nombre de lapins même quand il n'y en avait que 2 au début !

Se méfier des graphiques...

Quand on vous propose un graphique, regardez toujours les échelles utilisées et demandez-vous si cela vous donne la bonne impression ! Car, en prenant des chiffres identiques, on peut complètement changer l'impression qu'ils donnent en modifiant l'échelle utilisée. 

Un graphique en échelle logarithmique donne une impression très différente d'un graphique en échelle linéaire.
En échelle logarithmique, la population de lapins a l'air "d'augmenter gentiment"'... et, pourtant, ce n'est pas le cas puisqu'il suffit de dix ans pour passer de deux à mille millards de lapins !

Mais on peut aussi "fausser l'impression" en restant en échelle linéaire : il suffit de "bien" choisir où commence l'axe des y.

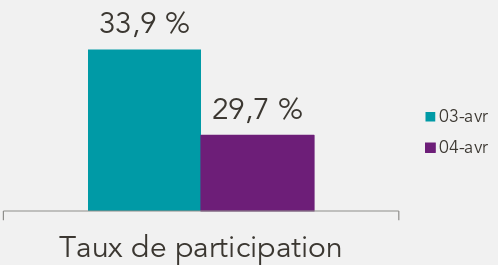Un exemple : dans un communiqué de presse, la SNCF donnait des nouvelles du taux de grévistes d'un jour à l'autre en avril 2018, en donnant cette image.

Source :
www.sncf.com/.../cp_taux_de_participation_4_avril_2018.pdf

Ouah, quelle plongée...

... sauf que si on représente cette évolution sur une échelle un peu plus représentative, ça ne donne pas le même effet !

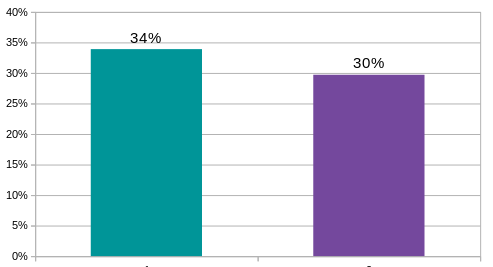
Voici les mêmes taux de grévistes (33,9% le 3 avril / 29,7% le 4 avril)

sur un axe des y allant de 0% à 35%	sur un axe des y allant de 0% à 100%

Et c'est le graphique qui prend les minumum et maximum possibles (aucun gréviste = 0% / tous en grève = 100%) qui est en fait le plus représentatif de la réalité.

Notez bien que cette façon de présenter les choses "à son avantage" n'est pas réservé à un organisme en particulier, il y en a mille exemples différents... Ne vous contentez jamais de l'impression que vous donne un grapique, regardez les chiffres !