 Inventer une liste de nombres qui aient l'air "pris au hasard" n'est pas si facile que ça...
Inventer une liste de nombres qui aient l'air "pris au hasard" n'est pas si facile que ça...
Pourtant, il suffit de respecter une loi mathématique très simple pour que la liste ne sente pas trop le trafiqué.
(Si vous voulez tester par quoi se trahit une "liste imaginaire", inventez 30 nombres de trois chiffres comme 243 ou 785, par exemple, et inscrivez-les sur une feuille avant de poursuivre la lecture)
Découverte d'une loi étrange
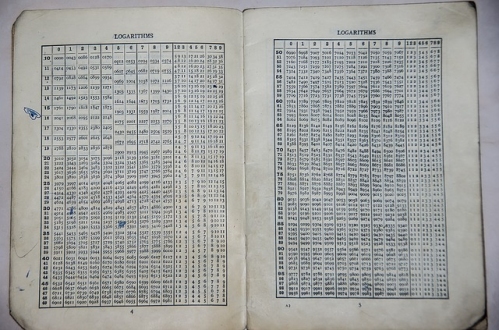 Il y a quelques années - avant que les calculatrices ne fleurissent dans tous les cartables - chaque bibliothèque scientifique possédait des exemplaires de "tables de logarithme".
Il y a quelques années - avant que les calculatrices ne fleurissent dans tous les cartables - chaque bibliothèque scientifique possédait des exemplaires de "tables de logarithme".
Ces livres donnaient dans des tableaux toutes les valeurs de la fonction "logarithme", un peu comme un recueil dans lequel on mettrait toutes les tables de multiplication.
Les premières pages rassemblaient les résultats commençant par "1", les suivantes les résultats commençant par "2", etc.
Ces livres servaient beaucoup aux scientifiques car on trouve la fonction logarithme dans de nombreuses lois physiques. Elle sert par exemple pour l'étude des changements d'état de la matière (les propriétés différentes de la glace, de l'eau et de la vapeur d'eau se calculent en utilisant une fonction logarithme). Mais elle sert aussi aux chimistes, aux géomètres et à tous ceux qui manipulent beaucoup de nombres.
 En 1881, l'astronome et mathématicien Simon Newcomb remarque que toutes les tables de logarithme qu'il trouve dans les bibliothèques ont un point commun : les premières pages sont toujours plus usées et plus sales que les dernières pages.
En 1881, l'astronome et mathématicien Simon Newcomb remarque que toutes les tables de logarithme qu'il trouve dans les bibliothèques ont un point commun : les premières pages sont toujours plus usées et plus sales que les dernières pages.
 Une question obsédante commence alors à le travailler : "Pourquoi les pages correspondant aux petits nombres sont-elles plus sales que les pages correspondant aux grands nombres ?"
Une question obsédante commence alors à le travailler : "Pourquoi les pages correspondant aux petits nombres sont-elles plus sales que les pages correspondant aux grands nombres ?"
Il ne voit qu'une explication : les scientifiques travaillent plus souvent avec des nombres commençant par "1" que par "2", plus souvent avec des nombres commençant par "2" que par "3", et ainsi de suite.
Et il en conclut donc qu'au cours de leurs expériences les scientifiques rencontrent plus souvent des nombres commençant par un petit chiffre que par un grand chiffre.
C'est étrange, mais le savant ne se laisse pas démonter et cherche à décrire ce phénomène. Il propose donc une équation mathématique pour décrire le total des nombres commençant par 1, 2, 3, ...8 et 9 :
|
La probabilité (p) que x (x=1, 2, ...,9) soit le premier chiffre significatif d'un nombre est
|
le premier chiffre significatif d'un nombre est son premier chiffre différent de zéro |
|
Par exemple, le nombre "32" Mais, quelle que soit la façon de l'écrire, |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Simon Newcomb publie sa découverte... mais peu de gens s'y intéressent.
 Cinquante-sept ans plus tard, le physicien Franck Benford refait la même observation, toujours à partir des tables de logarithme, et il retrouve la même équation que Newcomb.
Cinquante-sept ans plus tard, le physicien Franck Benford refait la même observation, toujours à partir des tables de logarithme, et il retrouve la même équation que Newcomb.
 Très intrigué, il passe plusieurs années à collecter des listes de nombres. Il décortique tous les documents qui lui passent sous la main et relève les nombres qui y apparaissent : la surface des pays, la longueur des rivières, les cours de la Bourse, le poids atomiques des éléments, les nombres apparaissant dans les articles des journaux, etc. Il rassemble ainsi 2029 inventaires, classe toutes les données et compte combien de nombres commencent par "1", puis "2", puis "3" ...
Très intrigué, il passe plusieurs années à collecter des listes de nombres. Il décortique tous les documents qui lui passent sous la main et relève les nombres qui y apparaissent : la surface des pays, la longueur des rivières, les cours de la Bourse, le poids atomiques des éléments, les nombres apparaissant dans les articles des journaux, etc. Il rassemble ainsi 2029 inventaires, classe toutes les données et compte combien de nombres commencent par "1", puis "2", puis "3" ...
Et lui aussi, retrouve que dans ses listes de nombres, il y en a plus qui commencent par 1 que par 2, par 2 que par 3, par 3 que par 4, etc. Il publie ses résultats en 1938 dans un article qui a la chance d'intéresser beaucoup plus de lecteurs que celui de Simon Newcomb... et la loi devient "la loi de Benford" (le monde est injuste !).
Certains mathématiciens ont voulu faire la démonstration de cette loi, mais aucun n'y est arrivé jusqu'à présent. Par contre, depuis les 2029 inventaires de Benford, les exemples de listes de nombres qui concordent avec cette loi se multiplient.
Vous voulez tester ?
 |
Prenez un magazine ou un journal. Pour cette liste, et celle que vous avez inventé, comptez (pour chaque liste) combien de nombres commencent par 1, par 2, par 3, etc. Inscrivez tes résultats dans le tableau... et comparez à ce que prévoit la loi. |
| premier chiffre | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| liste du magazine | |||||||||
| ta liste "inventée" | |||||||||
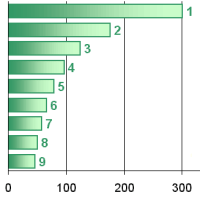
| prévision de la loi de Benford | 10 | 6 | 4 | 3 | 2 ou 3 | 2 ou 3 | 2 | 1 ou 2 | 1 |
La liste extraite des journaux a sans doute plus de nombres commençant par des petits chiffres que par des grands et la liste inventée, à peu près autant de chaque. Exact ?
Une loi utile pour repérer les fraudeurs !
Cette comparaison entre "vraie" liste et liste inventée permet de repérer les personnes qui donnent de faux chiffres.
Cette application de la loi de Benford est utilisée, par exemple, pour repérer les comptables qui essaient de truquer les finances d'une entreprise : on prend des nombres au hasard dans leur comptabilité et on vérifie qu'ils concordent avec la loi de Benford. Et si ce n'est pas le cas : on approfondit les recherches et on "épluche" toute la comptabilité !
Car, comme vous en composant vous-même votre liste de nombres, ces comptables sans scrupules se trahissent en citant - sans s'en rendre compte - beaucoup trop de nombres avec un premier chiffre significatif élevé.
Un signe qui ne trompe pas : il y a toujours beaucoup trop de 5 et de 6 (peut-être parce que ce sont les "chiffres du milieu") mais jamais assez de 1. Maintenant vous êtes avertis !
 A quelques modifications près, j'ai écrit cet article pour Sciences et Vie Junior.
A quelques modifications près, j'ai écrit cet article pour Sciences et Vie Junior.
Merci à François Boucq pour ce dessin qui illustrait l'article original
( Sciences et Vie Junior n° 119 - Août 1999)






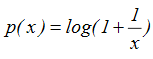


 Vous avez une question... et Archi7 n'y a pas encore répondu ?
Vous avez une question... et Archi7 n'y a pas encore répondu ?