Coulera ?
Coulera pas ?

Le sort de ce grain de raisin plongé dans l'eau dépend de sa flottabilité, une notion liée à la poussée d'Archimède qui explique aussi pourquoi un bateau en acier ne coule pas alors que l'acier est plus lourd que l'eau !

Un objet flotte s'il est plus léger que l'eau qu'il déplace et coule s'il est plus lourd

Prenons un bac rempli d'eau et 3 boules qui ont le même volume MAIS chacune une masse différente.
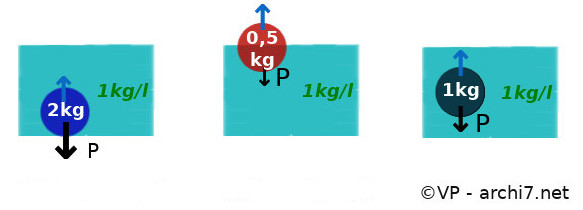
Disons par exemple que les boules ont toutes un volume de 1 litre mais des masses de 0,5 kg, 1 kg et 2 kg (c'est tout à fait possible si elles sont faites de matériaux différents).

Si on met ces boules au fond d'un bac d'eau, elles déplacent toutes les trois la même masse d'eau : 1 kg (puisqu'elles ont un volume de 1 litre et que 1 litre d'eau a une masse de 1 kg).
Mais...

la boule de 2 kg est plus lourde que l'eau qu'elle déplace, donc elle reste au fond	la boule de 0,5 kg est moins lourde que l'eau qu'elle déplace, donc elle remonte et flotte à la surface	la boule de 1 kg a la même masse que l'eau qu'elle déplace, donc elle "nage", comme si elle était elle aussi de l'eau...
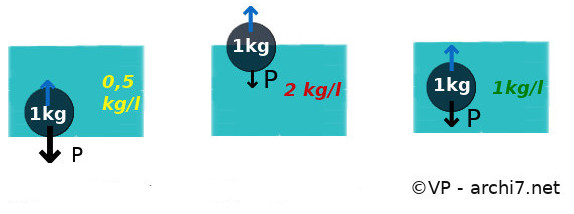
Inversons la situation ! Cette différence se retrouve aussi si on prend une même boule (ici de 1 kg) et qu'on la plonge dans des liquides qui trois masses différentes pour chaque litre de liquide déplacé !
Et si les liquides ont trois masses différentes assez proches pour chaque litre de liquide déplacé, la boule de 1 kg flotte plus au moins profondément

On récapitule !
Flottabilité d'un objet de masse m entièrement plongé dans un liquide de masse m_liquide pour un même volume que l'objet :

• si m < m_liquide : l'objet remonte,
  
• si m = m_liquide : l'objet nage entre deux eaux,
• si m_eau > m_liquide : l'objet coule.

Le cas particulier des bateaux et autres objets "lourds" qui flottent quand même !

"Posé sur l'eau", un objet creux ou concave déplace un volume d'eau qui a une masse supérieure à la sienne... donc il flotte !

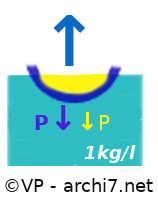C'est le cas d'un bateau en acier par exemple :
il déplace un volume V₁ fait d'acier (plus lourd que le même volume d'eau)
ET un volume V₂ dans sa coque,
donc au total un volume V = V₁ + V₂

La masse qui va déterminer la flottabilité du bateau est donc la masse totale M = m₁ + m₂
(où m₁ est la masse du volume V₁ et m₂ est la masse du volume V₂)
comparée à la masse en eau m_eau du volume V :

le bateau flottera si M < m_eau

• Si le bateau est vide : le volume V₂ est occupé par de l'air (très léger par rapport à l'eau), pas de souci, le bateau flotte !
• Si on le remplit d'une cargaison, il faudra veiller à ne pas mettre du "trop lourd" (sinon m₂ augmente dangeureusement la somme M = m₁ + m₂ et risque de la rendre plus grande que m_eau ! )
• Si le bateau se remplit d'eau, la situation est que - finalement - on n'a plus qu'un volume V₁ plongé dans de l'eau.
  Il faut donc comparer m₁ et m_eau (pour ce volume V₁) : avec une coque en acier, m₁ > m_eau donc le bateau coule !
  

 Quelques remarques :

• Si le bateau est fait en liège ou dans un matériau plus léger que l'eau, il ne coulera jamais :
  si on le remplit d'eau, m₁ reste inférieur à m_eau
  si on y met une très lourde charge : M = m₁ + m₂ sera supérieur à m_eau donc 'ensemble s'enfoncera dans l'eau MAIS la coque va tourner sur elle même, "laisser tomber" sa charge... et remonter à la surface !
• Au fur et à mesure qu'on charge un bateau, il s'enfonce dans l'eau donc les volumes V₁ et V₂ changent !
  Pour la flottabilité, c'est le résultat après équilibre qui compte.
  Si vous êtes déjà monté dans une barque, vous l'avez expérimenté : le bateau s'enfonce beaucoup quand vous arrivez... plus remonte un peu : les volumes se sont ajustés !
  De même, si vous vous glissez dans cette jolie bouée rose, elle s'enfonce une fois que vos bras sont appuyés dessus... et c'est le volume V₁ que vous faites "plonger" sous la surface de la piscine qui provoque la poussée d'Archimède qui vous porte !
• Pour un objet dans l'air (ou dans n'importe quel autre gaz), on peut aussi faire ce raisonnement à partir des masses déplacées pour savoir s'il s'envolera ou pas.
  mais, pour un objet dans un gaz, on parle plutôt de portance du gaz (on réserve le terme de "poussée d'Archimède aux liquides) :
  
  • si m < m_gaz : l'objet monte
  • si m = m_gaz : l'objet flotte dans le gaz (sans descendre ni monter),
  • si m > m_gaz : l'objet descend.
• Le raisonnement à partir des masses déplacées par un volume donné revient à réfléchir sur la masse volumique.
  La masse volumique est justement la masse occupée par un mètre cube, que l'on note ρ (la lettre grecque r prononcée rho), exprimée en kg / m³.
  ( voir la page masse volumique et densité pour plus de détails)
  Pour un objet entièrement plongé dans un liquide ou un gaz, on peut alors comparer directement leurs densités volumiques :
  
  • si ρ < ρ_{liquide ou gaz} : l'objet monte
  • si ρ = ρ_{liquide ou gaz} : l'objet "nage" (sans monter ni descendre),
  • si ρ > ρ_{liquide ou gaz} : l'objet descend.
    
  C'est ainsi que l'on réfléchit, par exemple, pour expliquer pourquoi une montgolfière s'envole ou comment fonctionne un thermomètre de Galilée !