 On peut décrire précisément comment un objet bouge.
On peut décrire précisément comment un objet bouge.
Merci Galilée et Newton !
Voici comment s'écrivent les mouvements, sur une ligne droite.
Les plus simples et très fréquents en sport (natation, course) et dans les transports (vélo, voiture, train).
Connaître les équations du mouvement linéaire (sur une ligne) d'un objet ou d'une personne est très utile !
Cela permet par exemple de calculer combien de temps il faut pour aller d'un point à un autre, ou quelle accélération un moteur de train doit fournir pour atteindre sa vitesse maximale dans un délai raisonnable, ou quelle distance il faut pour freiner.
 Galilée a fait beaucoup d'expériences sur le mouvement des billes : il les regardait accélérer, continuer à rouler puis s'arrêter. Et il a ainsi décrit très précisément comment elles se comportaient en ligne droite.
Galilée a fait beaucoup d'expériences sur le mouvement des billes : il les regardait accélérer, continuer à rouler puis s'arrêter. Et il a ainsi décrit très précisément comment elles se comportaient en ligne droite.
Et c'est Newton qui a fait vraiment avancer cette "science du mouvement", que l'on appelle d'ailleurs maintenant "mécanique newtonienne". Car il a décrit ce qui se passait en équations, en inventant pour cela une nouvelle façon de faire des mathématiques !
Mais commençons par voir ce que veulent dire exactement les trois infomations indispensables : la position, la vitesse et l'accélération !
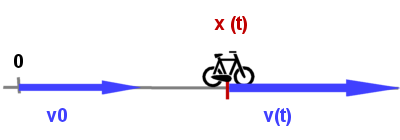
La position : x

On se place sur une ligne droite. Il suffit donc de mesurer où on est par rapport à un point de départ O (la lettre O).
On appelle cette distance x et on la mesure en mètres.
Et comme elle dépend du temps (t) on va l'écrire x(t).
La position est l'endroit où l'on est.
La vitesse : v
 On s'est déplacé pour aller de 0 à x(t) et il nous a fallu t secondes.
On s'est déplacé pour aller de 0 à x(t) et il nous a fallu t secondes.
On a ainsi parcouru x(t) mètres en t seconde.
Notre vitesse entre ces deux points a donc été x(t) / t mètres par seconde.
C'est notre vitesse moyenne.
 Arrivé au point x(t), on a une vitesse v(t) : c'est le nombre de mètres par seconde que l'on fait, à ce moment-là.
Arrivé au point x(t), on a une vitesse v(t) : c'est le nombre de mètres par seconde que l'on fait, à ce moment-là.
La vitesse est la façon dont la position change en fonction du temps :
v(t) s'écrit en mètres par seconde.
 On va appeler v0 la vitesse qu'on avait en O.
On va appeler v0 la vitesse qu'on avait en O.
Si on a roulé toujours à la même vitesse entre O et x(t), v(t) = v0 = x(t) / t
On dit que la vitesse est constante (les deux flèches bleues sont identiques).
 Mais notre vitesse a aussi pu changer.
Mais notre vitesse a aussi pu changer.
Soit parce qu'on a freiné : la vitesse v(t) en x(t) est plus petite que v0
Soit parce qu'on a accéléré : la vitesse v(t) en x(t) est plus grande que v0
On va décrire cela avec l'accélération.
L'accélération : a
 L'accélération est la façon dont la vitesse change en fonction du temps :
L'accélération est la façon dont la vitesse change en fonction du temps :
a(t) s'écrit en mètres par seconde par seconde.
Maintenant, à chaque instant t, on a trois informations pour notre vélo : sa position x(t), sa vitesse v(t) et son accélération a(t).
On peut à nouveau regarder ses changements de vitesse, en regardant ce que ça donne pour son accélération :
- s'il a toujours gardé la même vitesse entre O et x(t) : son accélération a été nulle
- s'il a freiné, sa vitesse a diminué : v(t) = v0 - (sa diminution de vitesse à chaque seconde x le nombre de secondes).
- s'il a accéléré, sa vitesse a augmenté : v(t) = v0 + (son augmentation de vitesse à chaque seconde x le nombre de secondes).
 Mais en fait, on va écrire une équation qui est juste dans tous les cas
Mais en fait, on va écrire une équation qui est juste dans tous les cas
v(t) = v0 + a.t
avec
- a est négatif si on freine (la vitesse diminue chaque seconde)
- a est positif si on accélère (la vitesse augmente chaque seconde)
- a est nul si on garde toujours la même vitesse
 Qu'il soit positif ou négatif, on appelle toujours ce "a" l'accélération (même quand ça freine ! ).
Qu'il soit positif ou négatif, on appelle toujours ce "a" l'accélération (même quand ça freine ! ).
Dans la vie quotidienne, quand on parle d'accélérer, on pense "aller plus vite". Mais en physique, le mot "accélérer" est neutre... ça peut faire gagner de la vitesse ou en faire perdre ! Parfois, on fait la différence entre "a positif" qui est une accélération et "a négatif" qui est une "décélération". Mais avec le mot "accélération" tout seul, on n'est jamais sûr....
 L'accélération n'est pas forcément toujours la même.
L'accélération n'est pas forcément toujours la même.
On peut freiner un peu puis tout à coup freiner plus fort. Ou accélérer beaucoup en démarrant son vélo puis continuer à augmenter sa vitesse, mais plus lentement. On peut aussi tout simplement accélérer au démarrage, gangner de la vitesse, puis rouler à vitesse constante et enfin freiner...
Bref, l'accélération dépend donc aussi du temps t.
L'équation la plus générale possible n'utilise pas simplement une accélération a constante mais a(t). Dans ce cas, la vitesse s'écrit : v(t) = v0 + a(t).t
Repasser de la vitesse à la position
Maintenant qu'on connaît la vitesse du vélo à chaque seconde, on peut aussi calculer sa position à chaque seconde, justement grâce aux écritures mathématiques qu'a inventé Newton (mais on ne donnera pas les détails ici du calcul intégral, seulement le résultat)
Nous allons supposer que l'accélération est constante, pour pouvoir faire un calcul simple.
En termes scientifiques, nous regardons ainsi un "mouvement rectiligne uniformément accéléré"
On a donc :
- une accélération constante a
- la vitesse qui s'écrit v(t) = v0 + a.t
- on peut en déduire (par intégration) : x(t) = v0 . t + a(t) . t2 / 2
L'ensemble de ces 3 équations s'appellent "les équations du mouvement" de notre vélo.
Vous en trouverez une application sur ce site, sur la page Y a-t-il une relation mathématique entre distance de freinage et vitesse ?
Ecriture plus générale des équations du mouvement
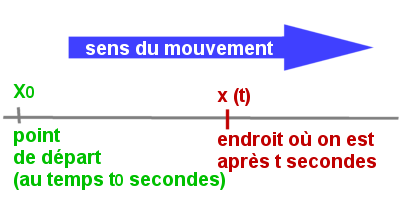 Remarquons :
Remarquons :
- qu'on n'est pas obligé de choisir le point O comme "point de départ" de la mesure des distances. On peut dire aussi que le point O n'est pas au point "zéro" mais que sa position est x0
- qu'on n'est pas non plus obligé de compter le temps à partir du moment où on passe au point x0 : ce moment est alors appelé t0.
On obtient alors les équations du mouvement rectiligne uniformément accéléré dans leur forme la plus générale possible :
- a = constante
- v(t) = v0 + a (t - t0)
- x(t) = x0 + v0 . t + a(t) . t2 / 2
Ces équations peuvent servir à décrire n'importe quel mouvement en ligne droite, à plat ou sur une pente.

 Mais il y aura une différence entre ces deux cas si on cherche à savoir POURQUOI le mouvement a lieu :
Mais il y aura une différence entre ces deux cas si on cherche à savoir POURQUOI le mouvement a lieu :
Newton a prouvé que l'accélération d'un objet (a) dépendait de sa masse (m) et de l'ensemble des forces (F) qu'il subissait : F = m x a.
Il faut donc faire un inventaire de toutes les forces. Et le poids agit différemment si on est sur une pente.







 Vous avez une question... et Archi7 n'y a pas encore répondu ?
Vous avez une question... et Archi7 n'y a pas encore répondu ?